⬅️Back
#h-a #TODO

DEFINITION

DEFINITION - CLASSIC

Mass Conservation Law applied to Flux #ASK

DEFINITION - SPECIAL RELATIVITY

$\mathrm{\forall }$ IRF

"RAZIO"

"RAZIO" - CLASSIC PHYSICS

1. Take a closed surface $S$. Inside it, there is a total Charge $q$ (that can be exchange w/ the outside) made of:
   • Static charges $q_L$
   • Moving charges $j_L$ ($\overrightarrow{j}=n\cdot q\cdot \overrightarrow{v}$)

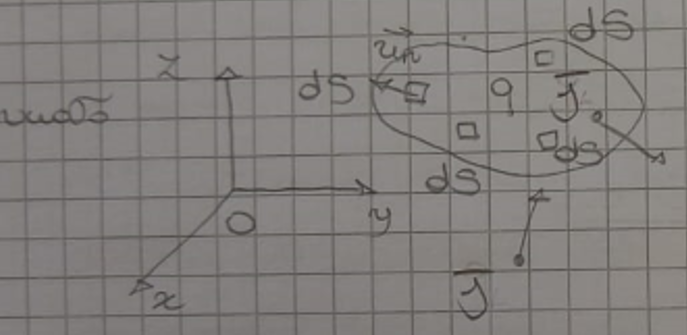
2. Divide surface $S$ in smaller $dS$ w/ Normal Vector exiting $S$.
3. Calculate Flux charges going through $dS$: $$\Phi=\oint_S\vec{j}\cdot\widehat{u}_n\cdot dS= -\frac{dq}{dt} → \oint_S\vec{j}\cdot\widehat{u}_n\cdot dS + \frac{dq}{dt}=0$$Where:
- IF charges are exiting → Flux $\mathrm{\Phi }$<0 → ↓$q$
- IF charges are entering → Flux $\mathrm{\Phi }$>0 → ↑$q$
4. Apply 1° Maxwell Equation to find total Charge $q$ → ${\oint }_S\overrightarrow{E}\cdot \cdot d\overrightarrow{S}=\frac{q}{{ϵ}_0}$ → $q={\oint }_S{ϵ}_0\cdot \overrightarrow{E}\cdot d\overrightarrow{S}$
5. Substitute and resolve → ${\oint }_S\overrightarrow{j}\cdot {\hat{u}}_n\cdot dS+\frac{d}{dt}({\oint }_S{ϵ}_0\cdot \overrightarrow{E}\cdot d\overrightarrow{S})=0$ → $$\oint_S \left(\vec{j} +\epsilon_0\cdot \frac{\partial\vec{E}}{\partial t} \right)\cdot d\vec{S}=0$$

"RAZIO" - SPECIAL RELATIVITY

1. Classically $\mathrm{\nabla }\cdot \overrightarrow{j}$ = ${\partial }_{x^k}{j}^k$
2. We are working w/ Four-Current $j^{\mu }=\left[\begin{array}{cc}c\cdot \rho & \overrightarrow{j}\end{array}\right]$ → $÷\cdot j^{\mu }$ = ${\partial }_{x^0}{j}^0+{\partial }_{x^k}{j}^k$ = #TODO

#h-t LINKED